Əvvəla mən Fibonaççi ədədləri haqqında məlumat vermək istərdim və bununçün də Vikipediaya müraciət edirəm:
«Riyaziyyatda, Fibonaççi ədədləri aşağıdakı kimi təyin olunur:
Tərifə əsasən, ilk iki Fibonaççi ədədləri 0 və 1-dir. Sonra gələn ədəd özündən əvvəlki ilk iki qonşusunun cəminə bərabərdir. Bəzi mənbələrdə sıranın ilk ədədi 0 yox, 1 götürülür.
Riyazi dildə, Fibanoççi sırası Fn aşağıdakı rekkurent düsturla verilir harda ki, F0 = 0 və F1 = 1.
Fibonaççi sırası Pizali Leonardonun adı ilə bağlıdır.
Davamı →

İbtidai icma quruluşunda yaşayan insanlar öz təkmilləşməmiş nəzərlərini tək-tək əşya deyil,əşya çoxluğuna salmışlar.İnsan cəmiyyəti,məsələn,heyvan sürüsünü,quşların dəstəsini,meşə ağaclarını və s. ayrı-ayrı əşyaya ayırınca uzun bir tarixi inkişaf yolu keçmişdir.İbtidai insanlar üçün sayılası əşyanın təkcə varlığı deyil,onların keyfiyyətlərinin də mühüm rolu olmuşdur.
Ardı →

Kimlər ki anadan riyaziyyatçı doğulmuşlar, yüksək ağıla malik olduqlarına görə, bütün başqa elmlərə yaxşı qabiliyyətləri var.

Sokrat (e.ə 469-399) yunan filosofu

Riyaziyyat ,təbiət öyrənməyə yaxşı və hətta yeganə girişdir.

D.İ.Pisarev(1840-1868) rus publisisti

Riyaziyyatın varlıq qüdrəti onun sahələrinin qırılmaz birliyindəndir.

D.Hilbert(1862-1943) alman riyaziyyatçısı

Ardı →

Dünyadakı ən məsum məşğuliyyət riyaziyyatdır.
Q.H.Hardi

İnsanlar ədədlər kimidir.O insanın dəyəri isə o ədədin içində olduğu ədəd ilə ölçülər.
İsaak Nyuton

Riyaziyyatda bir şeyləri əsla anlaya bilməzsən,yalnız onlara alışa bilərsən.
Con fon Neyman

Bir riyaziyyatçı fərz etməz, lakin bilər.İnandırmağa çalışmaz,çünki isbat edər.Etibarınızı gözləməz,bəlkə diqqət yetirmənizi istər.
Henri Poinkare
Davamı →

Hilbert (1862 — 1943)

Bir alman riyaziyyatçısı olan David Hilbert, 1862 ilində Königsberqdə anadan olmuşdur.1895 və 1929-cu illər arasında Qottingen Universitetində professor olmuşdur.XX əsrin əvvəlində Alman riyaziyyat məktəbinin başçısı hesab edilir.1897ci ildə cisim anlayışını və cəbri rəqəmlər qurmuşdur.1890cı illərdəki ilk çalışmaları sırasında,cəbri həndəsə və müasir cəbrdə əhəmiyyətli bir rol oynayan invariantlar nəzəriyyəsinin əsas qanunlarını ortaya çıxarmağı bacarmışdır.

Ardı →

İlk rəqəmlərin və say sistemlərinin meydana gəlməsi — Ədəd və ölçüyə aid anlayışların meydana gəlməsi Daş Dövrünə aid uzanır.Yüz min illərlə insanlar heyvanların yaşadığı vəziyyətdən fəqli olmayan bir şəkildə mağaralarda yaşamışlar.Öz enerjilərinin çoxunu yemək tapmağa sərf edirdilər.Ov etmək və balıq tutmaq üçün silahları,bir-biriləri ilə əlaqə qurmaq üçün isə danışıq dilini inkişaf etdirdilər.Daş Dövrünün sonlarına doğru yaradıcı sənətlərlə heykəllər və rəsmlər yaradaraq öz yaşayışlarını rəngləndirdilər.
Ardı →

Bu 5 məsələsdən 3-ü həndəsəyə,2-si cəbrə aiddir.

Ardı →

Kvadrat tənliyin xüsusi növlərini hələ babillilər 4000 il əvvəl həll etməyi bacarırdılar.Qədim yunan riyaziyyatçıları kvadrat tənliklərin ayrı-ayrı növlərini həndəsi qurmalara gətirməklə həll edirdilər.

Ardı →

Pi dünya riyaziyyat tarixinə təxminən e.ə. 2000-ci ildən bəri məlumdur. Ümumi olaraq onun rəqəmlə ifadəsi 3,14 kimi qəbul edilsə də, müxtəlif dövrlərdə onunla bağlı fərqli rəqəmlər səsləndirilib. Məsələn, misirlilər e.ə. 1650-ci ildə Pi-ni 3,165, çinlilər və yunanlar 3,162 olaraq hesablayıblar. Arximed isə iddia edib ki, Pi-nin dəyəri 310/71 və 31/7 arasında dəyişir.
Ancaq bununla bağlı araşdırmalar hələ də davam etməkdədir. Xüsusilə də kompyuter texnologiyasının sürətlə inkişaf etdiyi indiki dövrdə bu araşdırmalar daha da artıb. Məsələn, 2002-ci ildə Tokio Universitetində Pi-nin hesablanması üçün xüsusi kompyuter proqramı yazıblar.
Davamı →

Bir çoxüzlü bucaq götürək və onun bütün tillərini kəsən müstəvi keçirək. Çoxüzlü bucaqın S təpəsinin aid olduğu yarımfəzada SABDEF çoxüzlüsü alınır. Bu çoxüzlünün bir üzü ABCDEF çoxbucaqlısı qalan üzləri isə bir təpəsi S olan ortaq təpəsi üçbucaqlıdır. ASB, BSC,........, FSA, belə çoxüzlülər piramida adlanır.
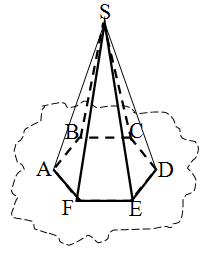
Ortaq təpəli üçbucaqlara piramidanın yan üzləri, onların birləşməsinə piramidanın yan səthi, çoxbucaqlıya piramidanın oturacağı, bütün yan üzlərin ortaq tərəfinə piramidanın yan tilləri, təpədən oturacaq müstəvisinə çəkilmiş perpendikulyara piramidanın hündürlüyü deyilir.
Bir üzü hər hansı çoxbucaqlı, qalan üzləri ortaq təpəli üçbucaqlar olan çoxüzlüyə piramida deyilir.
Piramida Oturacağındakı çoxbucaqlının adı ilə adlandırılır. Üçbucaqlı, dördbucaqlı, beşbucaqlı,… n bucaqlı piramida
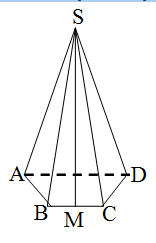
Yan üzdə təpədən oturacağın tərəfinə çəkilmiş hündürlüyə apofem deyilir.(SM)
Davamı →